Do LLMs Exhibit the Dunning-Kruger Effect
A recent experiment shows that LLMs are not good at solving complex logical problems like Cheryl's Birthday — but they think they are

Perhaps it’s the beginning of a slippery slope to use anthropomorphic terms when talking about AI but we all do: we talk about what LLMs think or what they know.
Because we may start to regard them as something close to sentient and thus more capable than we ought to expect.
Whereas, while LLMs contain enormous amounts of information and can perform complex tasks they are still just vast statistical machines churning out the next most probable token.
“The Dunning–Kruger effect is a cognitive bias in which people with limited competence in a particular domain overestimate their abilities” (Wikipedia). So, to assign a psychological trait like that to an LLM might seem wrong. However, it is a pretty accurate description of an LLM’s behaviour when it attempts to solve a problem that is beyond it.
“Cheryl’s Birthday” is a complex logical puzzle that is famous enough to have its own web page. It concerns three friends Albert, Bernard and Cheryl. Albert and Bernard want to know the date of Cheryl’s birthday, so Cheryl provides them with a set of clues.
The problem is stated as follows:
Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
May 15, May 16, May 19
June 17, June 18
July 14, July 16
August 14, August 15, August 17
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know too.
Bernard: At first I don’t know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.So when is Cheryl’s birthday?
The answer can be deduced by gradually rejecting impossible dates and requires some fairly sophisticated logical thinking (spoiler alert: it is July 16th — I’ve appended the complete solution to the end of the article.)
So how would an LLM like GPT-4 cope with this problem?
Fernando Perez-Cruz and Hyun Song Shin decided to find out and wrote their findings in “Testing the cognitive limits of large language models” [1]. They found that, when asked to solve the puzzle with the original wording, the LLM performed perfectly, correctly explaining the method for solving it and giving the correct answer.
However, when minor changes were made to the friends’ names or the names of the months, the AI failed.
Why was it that GPT-4 could work out a solution when it was presented in its original form but failed when inconsequential changes were made?
It’s in the data!
The answer is that the solution to Cheryl’s Birthday is well-known and is all over the internet — most obviously on Wikipedia. So the LLM did not need to perform any problem analysis, it just regurgitated the standard solution from its training data.
When the problem was re-presented the characters were changed to Jon, John and Jonnie, and the months became October, January, April and December. With this version of the problem (which is logically identical to the original) GTP-4 became confused and stated that “Jonnie’s birthday cannot be May or June”, referring to the month names from the original wording of the problem.
Thus the LLM was not properly addressing the puzzle but referring back to the text of the problem in its training data.
Beyond this, the LLM made logical errors that should have made further progress impossible and yet continued to produce a ‘solution’ to the problem that was clearly false.
As the authors point out this demonstrates two distinct failures: the first is a failure of reasoning which led it to follow a flawed process and the second, a lack of awareness of its own ignorance.
The way that the LLM gets things wrong and yet confidently comes up with a ‘solution’ is quite close to what is described by Dunning and Kruger[2].
Conclusion
Is it fair to try to characterise LLMs with psychological observations from humans?
Probably not but it wouldn’t be the first time it’s been done (see, for example, Thinking Fast and Slow in Large Language Models [3] which builds on Daniel Kahneman’s seminal work Thinking, Fast and Slow[4]).
But equally, we should remember that LLMs are flawed, maybe not in the same ways as humans, but still flawed. The experiment described above demonstrates two things:
First, while the answer that an LLM gives may be correct, it may not have been worked out the way you think it was. The response might simply be a regurgitation of training data not logical ‘thinking’.
Second, LLMs hallucinate not just by inventing non-existent things or events but by using logic that is not correct. Hallucination is, after all, simply a reflection of how LLMs work.
One last thing from the authors:
The irony is that once this bulletin is published and is available on the internet, the flawed reasoning reported in this bulletin will quickly be remedied as the correct analysis will form part of the training text for LLMs
Thanks for reading. If you want to see more of my stuff, follow me, or subscribe, on Medium or subscribe to this occasional (and free) Substack.
References
Testing the cognitive limits of large language models, Fernando Perez-Cruz and Hyun Song Shin, BIS Bulletin, No 83, 04 January 2024
Unskilled and Unaware of It: How Difficulties in Recognizing One’s Own Incompetence Lead to Inflated Self-Assessments, Justin Kruger and David Dunning, January 2000, Journal of Personality and Social Psychology 77(6):1121–34. You can find the full text on Researchgate.
Thinking Fast and Slow in Large Language Models, Thilo Hagendorff, Sarah Fabi, Michal Kosinski, arXiv:2212.05206
Thinking, Fast and Slow, Daniel Kahneman, 2013 (affiliate link)
The solution to Cheryl’s Birthday
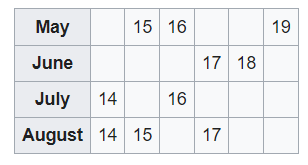
The solution to Cheryl’s Birthday is given in the paper[1] but Alex Bellos’s very clear version is given in Wikipedia. To start with the possible dates can be written in a grid:
Now here is the Bellos solution as presented by Wikipedia.
The answer can be deduced by progressively eliminating impossible dates.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know [either].
All Albert knows is the month, and every month has more than one possible date, so of course he doesn’t know when her birthday is. The first part of the sentence is redundant.
The only way that Bernard could know the date with a single number, however, would be if Cheryl had told him 18 or 19, since of the ten date options these are the only numbers that appear just once, as May 19 and June 18.
For Albert to know that Bernard does not know, Albert must therefore have been told July or August, since this rules out Bernard being told 18 or 19.
Bernard: At first I don’t know when Cheryl’s birthday is, but now I know.
Bernard has deduced that Albert has either August or July. If he knows the full date, he must have been told 15, 16 or 17, since if he had been told 14 he would be none the wiser about whether the month was August or July. Each of 15, 16 and 17 only refers to one specific month, but 14 could be either month.
Albert: Then I also know when Cheryl’s birthday is.
Albert has therefore deduced that the possible dates are July 16, Aug 15 and Aug 17. For him to now know, he must have been told July. If he had been told August, he would not know which date for certain is the birthday.
Therefore, the answer is July 16.